티스토리 뷰
1️⃣ 딥러닝 모델 학습의 문제점
실생활 문제 데이터의 차원이 증가하고, 구조가 복잡해졌다.
다양한 문제가 발생하게 되고 기술력의 부족으로 딥러닝 기술은 실질적인 한계를 마주하게 되었다.
1) 학습 속도 문제
: 데이터의 개수가 폭발적으로 증가하여 딥러닝 모델 학습 시 소요되는 시간도 함께 증가
2) 기울기 소실 문제
: 더 깊고 더 넓은 망을 학습시키는 과정에서 출력값과 멀어질 수록 학습이 잘 안되는 현상 발생
3) 초기값 설정 문제
: 초기값 설정 방식에 따른 성능 차이가 매우 크게 발생
4) 과적합 문제
: 학습 데이터(training data)에 모델이 과하게 최적화되어 테스트 데이터(test data)에 대한 모델 성능 저하
→ 1980년대 말 ~ 90년 중반 두번째 AI 빙하기
2️⃣ 학습 속도 문제와 최적화 알고리즘
GD(Gradient Descent)는 시작 지점에서 기울기의 반대 방향으로 하강하면서
손실 함수(loss function)를 최소화하는 지점을 찾기 위한 가장 직관적인 방법
→ 이처럼 전체 데이터 셋을 가지고 학습하게 되면 안정적이긴 하지만 계산량과 학습 비용이 많아진다.
(전체 학습 데이터 셋을 사용하여 손실 함수를 계산하기 때문에 계산량이 너무 많아진다.)

▶ 학습 속도 문제 해결 방법 : SGD
전체 데이터가 아닌 부분 데이터만 활용하여 손실 함수를 계산하자 → SGD (Stochastic Gradient Descent)
SGD (Stochastic Gradient Descent)
- 전체 데이터(batch) 대신 일부 조그마한 데이터의 모음인 미니 배치(mini-batch)에 대해서만 손실 함수를 계산

- 다소 부정확할 수 있지만, 훨씬 계산 속도가 빠르기 때문에 같은 시간에 더 많은 step을 갈 수있다.
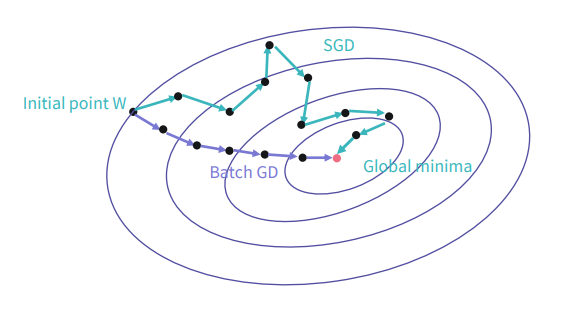
💡 GD vs SGD

SGD의 한계
1) Gradient 방향성 문제
: SGD는 gradient 값 계산 시, mini-batch에 따라 gradient 방향의 변화가 크다.
(손실 함수의 최솟값에 도달하는 동안 Gradient가 진동하여 최적값에 도달하기까지의 시간이 오래 걸린다.)
2) Learning Rate 설정 문제

▶ 다양한 최적화 알고리즘 등장

Momentum
- 과거에 이동했던 방식을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하는 방식

AdaGrad (Adaptive Gradient)
- 손실 함수(loss function)의 값을 최소로 만드는 최적의 가중치를 찾아내기 위해 learning rate를 조절해 하강하는 방법 중 하나
- 많이 변화하지 않은 변수들은 Learning rate를 크게 하고, 많이 변화했던 변수들은 Learning rate를 작게 하는 방식
- 과거의 기울기를 제곱해서 계속 더하기 때문에 학습이 진행될수록 갱신 강도가 약해진다.
- 기존 방식이 가중치들의 업데이트를 같은 속도로 한꺼번에 하는 방법이었다면,
Adagrad는 가중치 각각의 업데이트 속도를 데이터에 맞추어(adaptively) 계산해 적절한 learning rate로 하강
RMSProp
- 무한히 학습하다보면 순간 갱신량이 0에 가까워 학습이 되지 않는 Adagrad의 단점을 해결
(학습이 진행될수록 가중치 업데이트 강도가 약해지는 Adagrad의 단점 보완)
- 과거의 gradient 값은 잊고 새로운 gradient 값을 크게 반영해서 가중치 업데이트
Adam
- Momentum + RMSProp
- 가장 발전된 최적화 알고리즘
- 진행 방향과 learning rate 모두를 적절하게 유지하면서 학습할 수 있도록 고안
3️⃣ 기울기 소실 문제와 방지 기법
💡 기울기 소실 문제 (Vanishing Gradient)
깊은 층의 모델에서 역전파 시에 전달되는 손실 함수(loss function)의 gradient 값에
활성화 함수인 sigmoid 함수의 0에 가까운 기울기 값이 계속해서 곱해지면서 결국 가중치 업데이트가 잘 안되는 문제
딥러닝 모델 학습 방법은 목표 target 값과 실제 모델이 예측한 output 값이 얼마나 차이나는지 구한 후
오차값을 다시 뒤로 전파해가며 변수들을 갱신하는 알고리즘

기울기가 0인 값을 전달하며 중간 전달값이 사라지며 기울기 소실 문제(Vanishing Gradient) 발생
→ 기울기가 소실되는 문제가 반복되며 학습이 잘 이루어지지 않는다.
▶ 기울기 소실 문제 해결 방법 : ReLU
- 활성화 함수(Activation Function) 방식 변화
- 기존에 사용하던 sigmoid 함수 대신 ReLU 함수를 사용하여 해결

▶ 기울기 소실 문제 해결 방법 : Tanh
- 내부 Hidden Layer에는 ReLU를 적용하고 Output Layer에서만 Tanh를 적용

4️⃣ 초기값 설정 문제와 방지 기법
잘못된 초기값 설정 (초기화의 중요성)

가중치 초기화(Weight Initialization) 문제는 활성화 함수의 입력 값이 너무 커지거나 작아지지 않게 만들어주려는 것이 핵심이다.

▶ 초기화 설정 문제 해결을 위한 Naive한 방법
- 표준 정규분포를 이용해 초기화

- 표준편차를 0.01로 하는 정규분포로 초기화

▶ Xavier 초기화 방법 + Sigmoid 함수
- 표준 정규 분포를 입력 개수의 제곱근으로 나눈다.
- Sigmoid와 같은 S자 함수의 경우 출력 값들이 정규 분포 형태를 가져야 안정적으로 학습 가능하다.

▶ Xavier 초기화 방법 + ReLU 함수
- ReLU 함수에는 Xavier 초기화가 부적합하다.
- 레이어를 거쳐갈수록 값이 0에 수렴한다.

▶ He 초기화 방법
- 표준 정규 분포를 입력 개수 절반의 제곱근으로 나눈다.
- ReLU 함수와 He 초기화 방법을 사용했을 경우 그래프는 아래와 같다.
- 10층 레이어에서도 평균과 표준편차가 0으로 수렴하지 않는다.

▶ 적절한 가중치 초기화 방법
- Sigmoid, tanh의 경우 Xavier 초기화 방법이 효율적이다.
- ReLU계의 활성화 함수 사용 시 Xavier 초기화보다는 He 초기화 방법이 효율적이다.
- 최근의 대부분의 모델에서는 He 초기화를 주로 선택한다.
5️⃣ 과적합 문제와 방지 기법
💡 과적합(Overfitting)
: 모델이 학습 데이터에만 너무 치중되어 학습 데이터에 대한 예측 성능은 좋으나 테스트 데이터에 대한 예측 성능이 떨어지는 경우
- 모델이 과적합되면 일반화되지 않은 모델이라고 한다.

과적합이 발생하는 원인
1) 데이터의 퍼진 정도, 즉 분산(variance)이 높은 경우
2) 너무 많이 학습 데이터를 학습시킨 경우 (epochs가 매우 큰 경우)
3) 학습에 사용된 파라미터가 너무 많은 경우
4) 데이터에 비해 모델이 너무 복잡한 경우
5) 데이터에 노이즈 & 이상치(outlier)가 너무 많은 경우
▶ 딥러닝 모델 학습에서의 과적합 방지 기법
정규화(Regularization)
모델이 복잡해질수록 parameter들은 많아지고, 절댓값이 커지는 경향 발생
→ 기존 손실함수에 규제항을 더해 최적값 찾기 가능
L1 정규화(Lasso Regularization)

- 가중치의 절댓값의 합을 규제항으로 정의
- 가중치(weight)의 절댓값에 비례하는 손실(loss)이 기존 손실 함수(loss function)에 추가되는 형태
- 작은 가중치들이 거의 0으로 수렴하여 몇개의 중요한 가중치들만 남는다. → 모델을 일반화한다 (Sparse Model을 만든다)
(일부 가중치를 0으로 만들어 의미있는 가중치만 남긴다)
L2 정규화(Ridge Regularization)

- 가중치의 제곱의 합을 규제항으로 정의
- 가중치의 제곱에 비례하는 손실이 기존 손실 함수에 추가되는 형태
- 큰 값을 가진 가중치를 더욱 제약하는 효과
- L1 정규화에 비하여 0으로 수렴하는 가중치가 적음
(가중치의 값이 0에 가까워지도록 만든다. 가중치를 0으로 만드는 L1 정규화와는 차이가 있다.)
- 특정 가중치에 치중되지 않도록 가중치 값을 조율 → 가중치 감쇠 (Weight Decay)
드롭아웃(Dropout)
- 각 layer마다 일정 비율의 뉴런을 임의로 drop시켜 나머지 뉴런들만 학습하는 방법
- 데이터를 학습할 때, 일부 퍼셉트론(뉴런)을 랜덤하게 0으로 만들어 모델 내부의 특정 가중치(Weight)에 치중되는 것을 막는다
→ 모델이 일부 데이터에 가중되는 것을 막고 일반화된 모델을 만들 수 있다.
(학습이 끝난 후 테스트 과정에서는 드롭 아웃을 사용하면 안된다)
- 모델의 복잡도가 내려가면서 오버피팅이 덜 일어난다.
- 드롭아웃을 적용하면 학습되는 노드와 가중치들이 매번 달라진다.
- 다른 정규화 기법들과 상호 보완적으로 사용 가능하다.
- drop된 뉴런은 backpropagation 때 신호를 차단한다.
- Test 때는 모든 뉴런에 신호를 전달한다.

배치 정규화(Batch Normalization)
- Normalization을 처음 Input data 뿐만 아니라 신경망 내부 Hidden Layer의 input에도 적용
- 매 Layer마다 정규화를 진행하므로 가중치 초기값에 크게 의존하지 않는다. → 초기화 중요도 감소
- 과적합 억제 → Dropout, L1,L2 정규화 필요성 감소
- 핵심은 학습 속도의 향상


이 글은 엘리스의 AI트랙 5기 강의를 들으며 정리한 내용입니다.
'개발공부 > 🤖 DL & ML' 카테고리의 다른 글
| [자연어 처리] 텍스트 전처리 및 단어 임베딩 (0) | 2022.11.03 |
|---|---|
| [CNN] Convolutional Neural Network (0) | 2022.11.02 |
| [CNN] 이미지 데이터 (0) | 2022.11.01 |
| [딥러닝 기초] 텐서플로우와 딥러닝 학습 방법 (0) | 2022.10.28 |
| [딥러닝 기초] 퍼셉트론 (0) | 2022.10.25 |

프론트엔드 개발자 삐롱히의 개발 & 공부 기록 블로그