구간 합 (누적 합)

1️⃣  구간 합

합 배열을 이용하여 시간 복잡도를 줄이기 위한 알고리즘

 

 

 

합 배열 S

S[i] = A[0] + A[1] + ... + A[i-1] + A[i]

기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소

 

 

합 배열을 구하는 방법은

S[0] = A[0]
S[i] = S[i-1] + A[i]

 

 

예를 들어, 배열 A와 배열 A의 합 배열 S는 다음과 같다.

A = [1, 2, 3, 4, 5]

S = [1, 3, 6, 10, 15]

 

 

 

구간 합을 구하는 방법

배열 A의 인덱스 i부터 j까지의 구간 합을 구하고 싶다면

S[j] - S[i-1]

 

예를 들어, A = [15, 13, 10, 7, 3, 12] 라는 배열에서 A[2]부터 A[5]까지의 구간 합을 구하면

S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]

S[5] - S[1] = A[2] + A[3] + A[4] + A[5]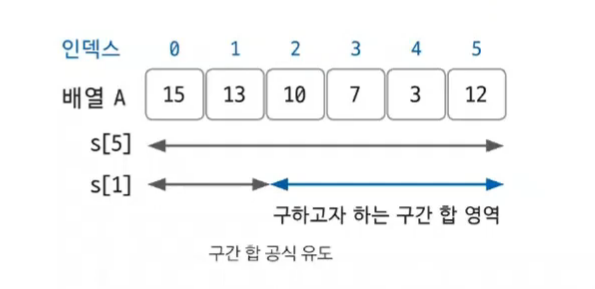

이미지 출처 : Do it! 알고리즘 코딩테스트 - 구간 합

 

 

 

 

합 배열 S는 기존 배열 A가 변하지 않는 이상 다시 구할 필요가 없다.

 

만약, 배열 A의 값이 자주 바뀐다면?

→ 세그먼트 트리 (인덱스 트리)

 

 

 

 

 

---

📌 구간 합 관련 문제들

 

✅  프로그래머스 Lv.2  -  연속된 부분 수열의 합

✅  백준  -  수들의 합 2

 

 

 

 

 

 

 

 

 

참고 자료

🔗 알고리즘 코딩테스트 핵심이론 강의 - 구간 합

🔗 [코딩테스트 공부] 수들의 합